Metody:
Metoda siatki kwadratów

Metoda polega na podzieleniu terenu na siatkę kwadratów (np. 10m x 10m, 5m x 5m lub inną. Im drobniejsza siatka tym dokładniejsze wyliczenia). Zaznaczamy linię oddzielającą wykop od nasypu. Następnie w każdym z oczek wyliczamy objętość masy ziemi (pole powierzchni figury * średnia wysokość narożników figury)
Jak to policzyć?
- Rysujemy siatkę kwadratów na mapce wysokościowej np. 10m x 10m
- W każdym z narożników każdego kwadratu sprawdzamy zapisujemy aktualną wysokość terenu oraz wysokość projektowaną. Możemy też od razu wyliczyć różnię tych wysokości i zapisać ją obok.
- Przez siatkę kwadratów może przebiegać tzw. linia zerowa robót ziemnych – jest to warstwica która pokrywa się z projektowanym poziomem terenu a więc wysokość terenu nie ulega tutaj zmianie. Linia zerowa oddziela nasyp oznaczany jako N od wykopu oznaczanego W. Kwadrat przedzielony linią zerową dzieli się na inne figury: trapez, trójkąt, pięciobok – wtedy w jednym oczku będziemy mieć kawałek wykopu i kawałek nasypu które policzymy osobno.
- Liczymy pole powierzchni figury. (kwadratu, trapezu, trójkąta prostokątnego lub pięcioboku)
- Wyliczone pole figury mnożymy przez uśrednioną wysokość narożników tej figury pamiętając że wysokość narożników przy linii zerowej wynosi 0.
Wzór ogólny:
V=pole\_figury ∗ \frac{suma\_narożników}{ilość\_narożników}Wzory dla poszczególnych figur:
Kwadrat:
V=a^2∗\frac{h1+h2+h3+h4}{4}Trójkąt:
V=\frac{a*b}{2}*\frac{h1}{3}Trapez:
V=(\frac{a+b}{2}*h)*\frac{h1+h2}{4}Pięciobok:
V=(a^2-\frac{a*b}{2}) * \frac{h1+h2+h3}{5}
Bilans ziemny
Bilans ziemny polega na podsumowaniu w specjalnej tabeli wszystkich wykopów i nasypów. Następnie po wyliczeniu różnicy okaże się czy brakuje nam ziemi na terenie inwestycji (bilans ujemny) czy mamy jej za dużo i będzie ją trzeba gdzieś wywieźć (bilans dodatni).

Przykładowe zadanie:
Zad. Ile wynosi objętość wykopu liczonego metodą siatki kwadratów z ilustracji poniżej?
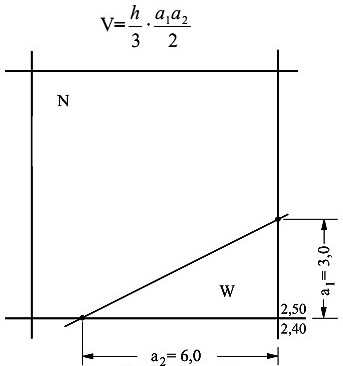
Odpowiedź: 0,3m3
Metoda przekrojów terenowych
Oblicz objętość mas ziemnych wykopu o długości 6 m i przekroju przedstawionym na rysunku.
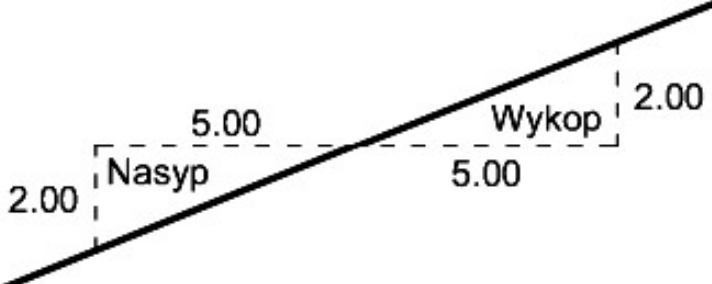
Zadania opisowe lub na podstawie szkicu
Na egzaminach pojawiają się również zadania wymagające obliczenia objętości wykopów/nasypów na podstawie szkiców lub opisu. Wykorzystywana tutaj jest umiejętność obliczania objętości podstawowych figur geometrycznych.
Przykłady zadań:
zad 1: Ile wynosi objętość wykopu, którego długość wynosi 5 m, a dwa skrajne przekroje mają powierzchnię 2 m2 i 4 m2?
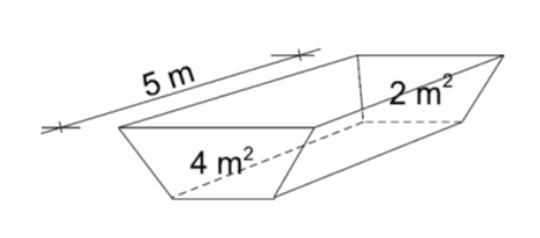
Żeby wyliczyć objętość wykopu należy wyciągnąć średnią z 2 przekrojów (w tym przypadku (2+4)/2=3m2) i pomnożyć razy odległość między przekrojami (5m). Czyli:
średnia pól przekrojów: (2m2+4m2)/2 = 3m2
średnia * odległość między przekrojami: 3m2 * 5m = 15m3
Taki typ zadania może wystąpić również bez ilustracji.
zad 2: Objętość masy ziemi pochodzącej z wykopu pokazanego na rysunkach wynosi
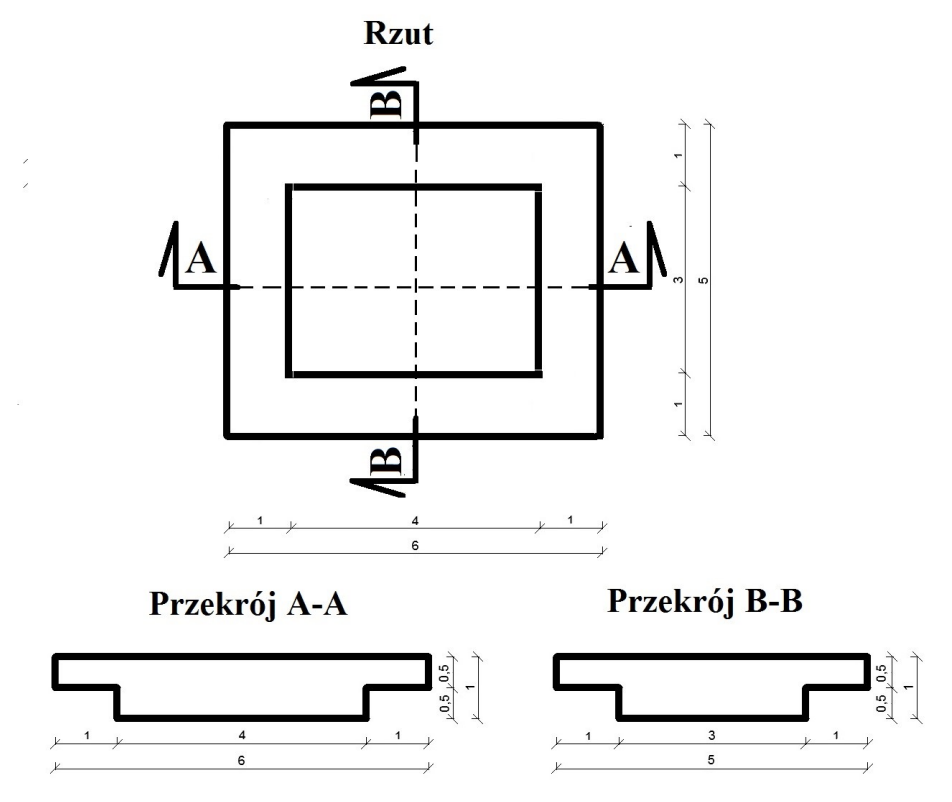
Rozwiązanie: Osobno liczymy objętość jednego równoległoboku np. położonego głębiej (3 x 4 x 0,5 = 6m3) oraz drugiego równoległoboku (5 x 6 x 0,5 = 15m3) i sumujemy ich objętości: 6m3 + 15m3 = 21m3.
zad.3: Jaką objętość ma wykop pokazany na szkicu (wymiary podano w metrach):
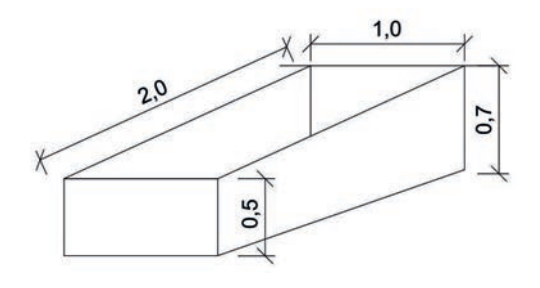
Zadanie możemy policzyć na 2 sposoby:
- Tutaj należy samodzielnie policzyć 2 pola powierzchni przekrojów i je uśrednić a następnie pomnożyć razy odległość między nimi: (1 x 0,5 = 0,5m2, 1 x 0,7 = 0,7m2, średnia = 0,6m2 * 2m = 1,2m3)
- Policzyć pole trapezu i pomnożyć razy wysokość
